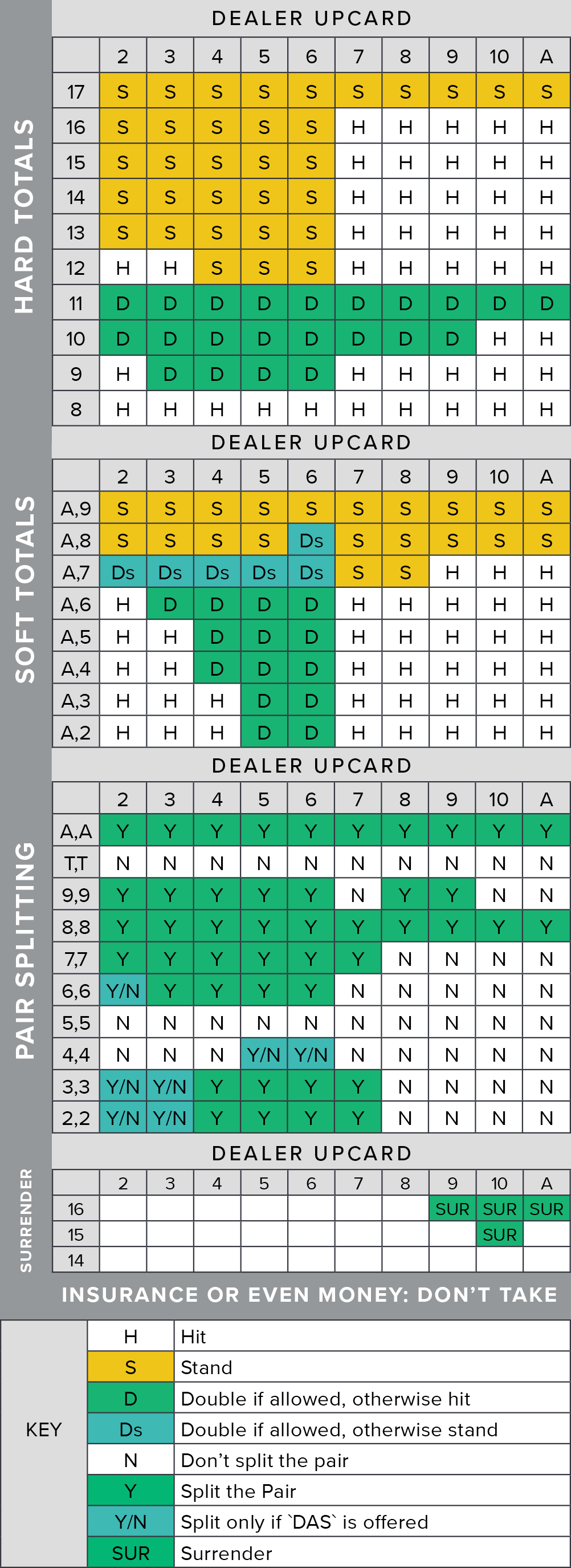
- Calculating Blackjack Probabilities
- Probability Blackjack Questions
- Blackjack Statistics And Probabilities
- Blackjack Probability Tables
Being dealt a 20 means 2 cards that are either an Ace and a 9 or two ten-value cards. The dealer’s 21 (blackjacks included) are: roughly 8% Your probability of being dealt 20 is approximately 9. In the classic Blackjack, players need to make their decisions by only seeing one of the dealer’s cards which is called the up card. Closest casino to me. If by any chance, they get to see it, this places them in a very advantageous position and their chances of winning are significantly increased. In principle, a pair of aces should of course be split, but in this case blackjack rules allow you to get only one card on each hand, and getting a 10 does not make a blackjack. With the basic strategy, you should never split 10's, 5's or 4's, always split 8's, and, in the other cases, split against an up card of 2.
'What percentage of hands are suited blackjacks? Six-deck shoe, any suit.
RWR FROM TUSCON, USA
The probability of a suited blackjack in a six-deck game is 2*(4/13)*(6/311) = 0.0118723.'
So for 5 decks (not that it will change, but just do the math): 2*(4/13)*(5/259) = .0118, or 1.18%, all the same.
Be sure to leverage the search functionality, or even Google (all I did was type 'odds of getting suited blackjack' and the Wizards page was the first hit).
1-0.3051= 69.49%
This is for 100 repeated trials of taking cards out of a fresh shoe. I'm not sure what is meant by '5 deck shuffler', but if cards are discarded each hand, that will change your probability. That calculation would be rather cumbersome without programming.
About 1 in 4 of those will be suited.
This rough math gets you to 1/84=0.0119 chance of a suited blackjack, which is very close with much less math.
.. which is very close with much less math.
Dieter, we're supposed to teach the kids that math is fun! =P
Dieter, we're supposed to teach the kids that math is fun! =P
It is! Math is great fun!
.. but useful approximations are at least as fun, and quite useful, and often easier to remember.
Every schoolkid should know that (about) 1 hand in 21 should be a blackjack. If you play, that's just something you should know. It should be obvious that 1 in 4 will be suited.
As for accuracy.. 1.187% vs 1.190% is darn close. 3 one thousandths of one percent close. Surely good enough for government work.
It's right up there with 'pi seconds is about a nanocentury'. (Of course, it's actually closer to 'square root of 10 seconds', but that's less fun.)
I'm not sure what is meant by '5 deck shuffler', but if cards are discarded each hand, that will change your probability. That calculation would be rather cumbersome without programming.
Based on how the question is phrased, I'd assume that the game is being played out of a 5-deck CSM. If you're not acquainted with them, they're pretty common machines in the US where the cards are fed back into the machine and reshuffled every few hands. Based on what I've seen, I'd estimate that, on average, ten cards will be in the discard at a given time. (Obviously, highly dependent on casino policy, number of hands, etc.)
It's close enough to playing with a constantly fresh n-deck game that the math shouldn't be thrown off by much though.
It is! Math is great fun!
.. but useful approximations are at least as fun, and quite useful, and often easier to remember.
Every schoolkid should know that (about) 1 hand in 21 should be a blackjack. If you play, that's just something you should know. It should be obvious that 1 in 4 will be suited.
As for accuracy.. 1.187% vs 1.190% is darn close. 3 one thousandths of one percent close. Surely good enough for government work.
It's right up there with 'pi seconds is about a nanocentury'. (Of course, it's actually closer to 'square root of 10 seconds', but that's less fun.)
Am I missing pi ~ 22/7 in that image? How could Randall forget that, or is it too obvious?
Am I missing pi ~ 22/7 in that image? How could Randall forget that, or is it too obvious?
355/113 is closer. 7 digits of accuracy in only 6 digits.
Or, 4*atan(1) (in radians).
355/113 is closer. 7 digits of accuracy in only 6 digits.
Or, 4*atan(1) (in radians).
1118CodificationTitles amended. Fincen requirements for casinos. Introduced in the House as H.R. . Currency be reported to the Department of the Treasury, and for other purposes.(colloquial)BSANicknamesFederal Deposit Insurance Act AmendmentsEnacted bytheEffectiveOctober 26, 1970CitationsPublic law84 aka 84 Stat.
The variety of mentioned extra chances that are winning makes the game even more inviting.The symbol of Ra is Wild, that means it can substitute the majority of the other symbols of Riches of RA Slot Game. But only after that idea comes another prosperity and by playing this game, you have a possibility of getting a number of the Egyptian riches.Players may win in Riches of RA Slot Game not only in a manner that is classic, hitting among 15 pay-lines. Free slots riches of ra. There is also a set of additional chances to increase. The most desired combination you can get is when three symbols of Ra pile up to fully cover the first and the fifth reel it gives you 15 Free Spins, where the mentioned reels stay Wild so, as you correctly suppose, you can acquire a nice sum of money then.Another additional option is triggered when three sculptures show up on the reels.
I agree 355/113 isbetter. 22/7 is just what we were told in some really basic math classes to use as an estimation.
4atan(1) = pi, not an approximation
- Page 1 of 2
Calculating Blackjack Probabilities
You have an awesome sight & I have enjoyed your articles for a few years now.. thank you for giving us this web site.
I am been running different numbers thru my head trying to come up with a way to compute the probabilities of getting 3 blackjacks in a row with a 6 deck continuous shuffle machine? Or even the odds of getting 5 blackjacks in a row with the same situation?
Also.. I saw a casino promotion where you got a drawing ticket every time you were dealt a red queen and a black ace.. is there a way to calculate my odds of getting this type of hand in blackjack?
Thank you
L8lori
Edit: FYI, from the Wizard's Blackjack page, the general formula for calculating the odds of a blackjack in n decks is: 2*(4/13)*(4n/(52n-1)).
From the Wizard of Odds Blackjack page, the probability of getting a blackjack on a six deck game is: 0.047489. The probability of this happening three times in a row is: (.047489)^3 = .00010709743 or 1 in 9,337
I'm glad it's that low, because I ever actually got three blackjacks in a row, the earth would open up and swallow me and the casino.
I'm glad it's that low, because I ever actually got three blackjacks in a row, the earth would open up and swallow me and the casino.
Jan 21, 2014 With Trish Regan. Trish Regan takes you inside the secret world of a Las Vegas high roller who wins millions at the casinos - and reveals how the gambling industry may be more beatable than you think. Learn how one gambler transformed himself from. The player secrets of a vegas whale.
I got two in a row a few days ago. I was all like 'yay! Blackjack again!'
Probability Blackjack Questions
I think I colored up after that, because I wanted to leave on a high point ;-)
The star casino gold coast dress code. I saw a casino promotion where you got a drawing ticket every time you were dealt a red queen and a black ace.. is there a way to calculate my odds of getting this type of hand in blackjack?
In a six deck shoe (or CSM) there are 12 red queens and 12 black aces. The odds of getting dealt one of each is (12/312)*(12/311) = .001484 or 1-in-674.
I'm glad it's that low, because I ever actually got three blackjacks in a row, the earth would open up and swallow me and the casino.
1-in-9,337 is not that unusual, when, according to the Wizard, the odds of getting a royal flush in VP, if all you did was try to get a Royal every draw are 1-in-23,081.
In a six deck shoe (or CSM) there are 12 red queens and 12 black aces. The odds of getting dealt one of each is (12/312)*(12/311) = .001484 or 1-in-674.
Blackjack Statistics And Probabilities
You neglected that the cards may be dealt in either order, so the probability is twice as great as you calculated.
You neglected that the cards may be dealt in either order, so the probability is twice as great as you calculated.
Blackjack Probability Tables
Thank you for the correction PapaChubby. This is my calculation: (24 (12 red Q's and 12 black A's) / 312 total cards in six decks) * (12 red Q's or black A's, depending on what was dealt first/311) = 1-in-337